2017年广东成人高考高起点文史财经类数学考试真
编辑整理:广东成考网 发表时间:2020-08-10 15:51:18 【大 中 小】
2017年成人高等学校高起点招生全国统一考试
数 学
本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分。满分150分。考试时间150分钟。
第I卷(选择题,共85分)
一、选择题(本大题共17小题,每小题5分,共85分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.设集合M={1,2,3,4,5),N={2,4,6),则M∩N=( )
A.{2,4) B.(2,4,6) C.(1,3,5) D.{1,2,3,4.5,6)
2.函数y=3sin 的最小正周期是( )
的最小正周期是( )
A.8π B.4π C.2π D.2π
3.函数y=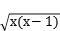 的定义城为( )
的定义城为( )
A.{x|x 0} B.{x|x
0} B.{x|x 1} C.{x|
1} C.{x|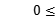 x
x 1} D.{x|
1} D.{x|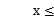 0
0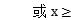 1}
1}
4.设a,b,c为实数,且a>b,则( )
A.a-c>b-c B.|a|>|b| C. >
> D.ac>bc
D.ac>bc
5.若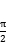 <
< <
< ,且sin
,且sin =
= ,则
,则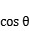 =( )
=( )
A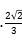 B.
B.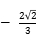 C.
C.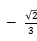 D.
D.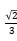
 6.函数y=6sinxcosc的最大值为( )
6.函数y=6sinxcosc的最大值为( )
A.1 B.2 C.6 D.3
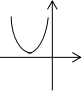
7.右图是二次函数y=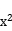 +bx+c的部分图像,则( )
+bx+c的部分图像,则( )
A.b>0,c>0 B.b>0,c<0 C.b<0,c>0 D.b<0,c<0 0
8.已知点A(4,1),B(2,3),则线段AB的垂直平分线方程为( )
A.x-y+1=0 B.x+y-5=0 C.x-y-1=0 D.x-2y+1=0
9.函数y= 是( )
是( )
A.奇函数,且在(0,+ )单调递增 B.偶函数,且在(0,+
)单调递增 B.偶函数,且在(0,+ )单调递减
)单调递减
C.奇函数,且在(- ,0)单调递减 D.偶函数,且在(-
,0)单调递减 D.偶函数,且在(- ,0)单调递增
,0)单调递增
10.一个圆上有5个不同的点,以这5个点中任意3个为顶点的三角形共有( )
A.60个 B.15个 C.5个 D.10个
11.若lg5=m,则lg2=( )
A.5m B.1-m C.2m D.m+1
12.设f(x+1)=x(x+1),则f(2)= ( )
A.1 B.3 C.2 D.6
13.函数y=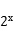 的图像与直线x+3=0的交点坐标为( )
的图像与直线x+3=0的交点坐标为( )
A.(-3,-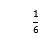 ) B.(-3,
) B.(-3,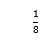 ) C.(-3,
) C.(-3,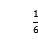 ) D.(-3,-
) D.(-3,-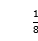 )
)
14.双曲线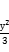 -
-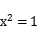 的焦距为( )
的焦距为( )
A.1 B.4 C.2 D.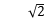
15.已知三角形的两个顶点是椭圆C: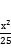 +
+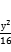 =1的两个焦点,第三个顶点在C上,则该三角形的周长为( )
=1的两个焦点,第三个顶点在C上,则该三角形的周长为( )
A.10 B.20 C.16 D.26
16.在等比数列{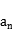 }中,若
}中,若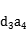 =10,则
=10,则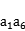 ,+
,+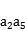 =( )
=( )
A.100 B.40 C.10 D.20
17.若1名女生和3名男生随机地站成一列,则从前面数第2名是女生的概率为( )
A.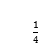 B.
B.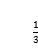 C.
C.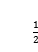 D.
D.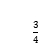
第Ⅱ卷(非选择题,共65分)
二、填空题(本大题共4小题,每小题4分,共16分)
18.已知平面向量a=(1,2),b=(-2,3),2a+3b= .
19.已知直线1和x-y+1=0关于直线x=-2对称,则1的斜率为= .
20.若5条鱼的平均质量为0.8kg,其中3条的质量分别为0.75kg,0.83kg和0.78kg,则其余2条的平均质量为 kg.
21.若不等式|ax+1|<2的解集为{x|- <x<
<x< },则a= .
},则a= .
三.解答题(本大题共4小题,共49分.解答应写出推理、演算步骤)
22. (本小题满分12分)
设{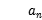 }为等差数列,且
}为等差数列,且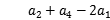 =8.
=8.
(1)求{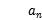 }的公差d;
}的公差d;
(2)若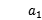 =2,求{
=2,求{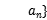 前8项的和
前8项的和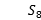 .
.
23.(本小题满分12分)
设直线y=x+1是曲线y=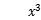 +3
+3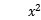 +4x+a的切线,求切点坐标和a的值。
+4x+a的切线,求切点坐标和a的值。
24.(本小题满分12分)
如图,AB与半径为1的圆0相切于A点,AB=3,AB与圆0的弦AC的夹角为50°.求
(1)AC:
 (2)△ABC的面积.(精确到0.01) C
(2)△ABC的面积.(精确到0.01) C
A B
25. (本小题满分13分)
已知关于x,y的方程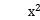 +
+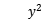 4xsin
4xsin -4ycos
-4ycos =0.
=0.
(1)证明:无论 为何值,方程均表示半径为定长的圆;
为何值,方程均表示半径为定长的圆;
(2)当 =
=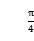 时,判断该圆与直线y=x的位置关系.
时,判断该圆与直线y=x的位置关系.
2017年成人高等学校高起点招生全国统一考试
数学(理工农医类)答案及评分参考
一、选择题
1.A 2.A 3.D 4.A 5.B 6.D 7.A 8.C 9.C 10.D 11.B 12.C 13.B 14.B 15.C 16.D 17.A
二、填空题
18. (-4,13) 19.-1 20.0.82 21.2
三、解答题
22.因为{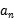 }为等差数列,所以
}为等差数列,所以
(1)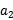 +
+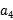 -2
-2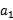 =
=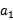 +d+
+d+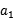 +3d-2
+3d-2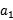
=4d=8,
d=2.
(2)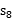 =
=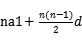
=2 8+
8+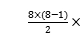 2
2
=72.
23.因为直线y=x+1是曲线的切线,所以y'=3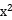 +6x+4=1.解得x=-1.
+6x+4=1.解得x=-1.
当x=-1时,y=0,
即切点坐标为(-1,0).
故0=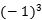 +3
+3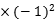 +4
+4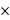 (-1)+a=0
(-1)+a=0
解得a=2.
24.(1)连结OA,作OD⊥AC于D.
 因为AB与圆相切于A点,所以∠OAB=90°. C
因为AB与圆相切于A点,所以∠OAB=90°. C
则∠0AC=90°=50°-40°.

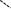 AC=2AD
AC=2AD
=2OA·cos∠OAC D
=2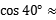 1.54. A B
1.54. A B
(2)S△ABC= AB·ACsin∠BAC
AB·ACsin∠BAC
=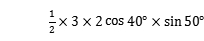
=3os240°
=l.78.
25. (1)证明:
化简原方程得
X2+4xsin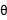 +4sin2
+4sin2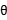 +y2-4y
+y2-4y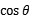 +4
+4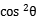 -4sin2
-4sin2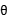 -4
-4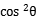 =0,
=0,
(36+2sin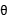 )2+(y-2cos
)2+(y-2cos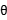 )2=4,
)2=4,
所以,无论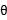 为何值,方程均表示半径为2的圆。
为何值,方程均表示半径为2的圆。
(2)当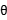 =
= 时,该圆的圆心坐标为O(-
时,该圆的圆心坐标为O(-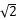 ,
,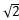 ).
).
圆心O到直线y=x的距离
d=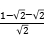 =2=r.
=2=r.
即当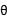 =
= 时,圆与直线y=x相切.
时,圆与直线y=x相切.
本文标签:广东成考文数2017年广东成人高考高起点文史财经类数学考试真
转载请注明:文章转载自(http://www.dgzkw.com)
⊙小编提示:添加【广东成考网】招生老师微信,即可了解2024年广东省成人高考政策资讯、成人高考报名入口、准考证打印入口、成绩查询时间以及领取历年真题资料、个人专属备考方案等相关信息!

(添加“广东成考网”招生老师微信,在线咨询报名报考等相关问题)
填写下方信息,领取广东成考《备考方案》!
《广东成考网》免责声明:
1、由于考试政策等各方面情况的调整与变化,本网提供的考试信息仅供参考,最终考试信息请以省考试院及院校官方发布的信息为准。
2、本站内容部分信息均来源网络收集整理或来源出处标注为其它媒体的稿件转载,免费转载出于非商业性学习目的,版权归原作者所有,如有内容与版权问题等请与本站联系。联系邮箱:812379481@qq.com。








 ×
×